Quantum computing has largely evolved around the concept of the qubit, a two-level quantum system that can exist in a superposition of the |0⟩ and |1⟩ states. However, the principles of quantum mechanics allow for more than just binary logic. Increasingly, researchers are exploring higher-dimensional quantum systems—qutrits (three-level systems) and ququarts (four-level systems)—as alternatives that could enhance performance, reduce hardware overhead, and improve fault tolerance in future quantum architectures.
A recent landmark study published in Nature (2025) demonstrated, for the first time, error correction protocols applied successfully to qutrits and ququarts. This proof of concept represents a critical step toward generalizing quantum error correction and potentially overcoming one of the most persistent bottlenecks in the field: noise and decoherence.
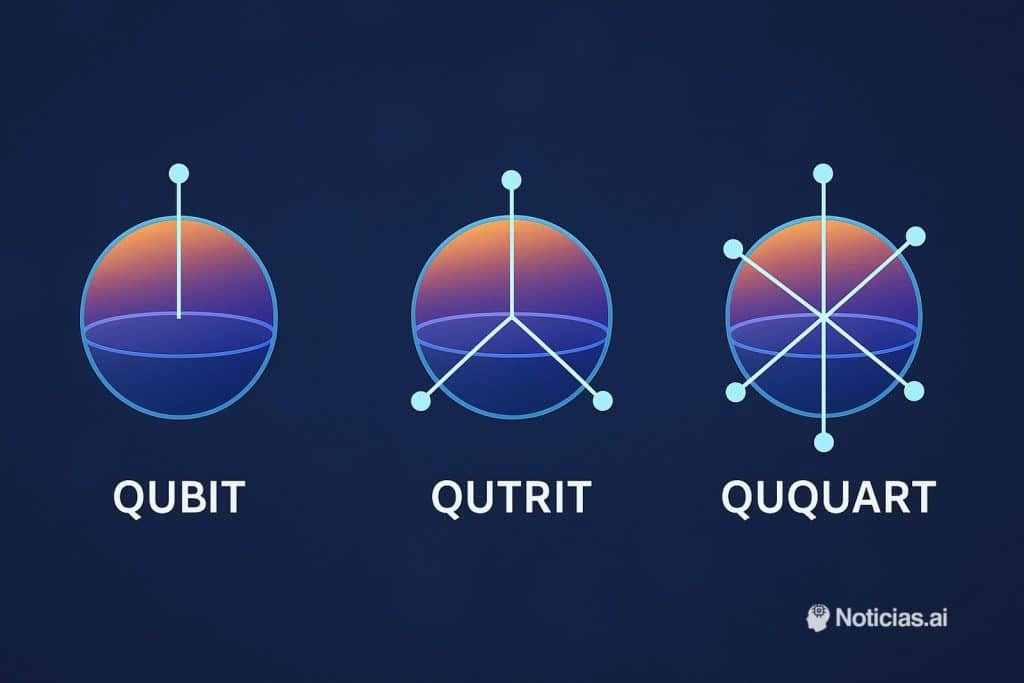
From Qubits to Qudits
In quantum information theory, the term qudit refers to any d-level quantum system. These generalize the qubit:
- Qubit: 2 states — |0⟩, |1⟩
- Qutrit: 3 states — |0⟩, |1⟩, |2⟩
- Ququart: 4 states — |0⟩, |1⟩, |2⟩, |3⟩
Instead of restricting the Hilbert space to two dimensions, qudits expand the computational space exponentially with fewer physical units, enabling denser encoding of information and potentially more compact quantum circuits.
Why Are Qudits Underutilized?
Despite their theoretical advantages, qudits—particularly qutrits and ququarts—are not yet mainstream in hardware implementations due to several practical challenges:
- Control Complexity: Qudit gates require more sophisticated manipulation, often beyond current control electronics and pulse-shaping techniques.
- Hardware Constraints: Many quantum platforms, such as superconducting transmons or trapped ions, are optimized for two-level transitions and require non-trivial redesigns to stably isolate and manipulate higher energy states.
- Increased Error Sensitivity: Additional levels reduce the energy spacing between states, increasing the likelihood of thermal or environmental disturbances leading to state leakage or decoherence.
- Algorithmic Incompatibility: Most current quantum algorithms, including Grover’s or Shor’s, are formulated in binary logic and need to be reformulated for qudit logic, which remains an open research area.
The 2025 Breakthrough: Error Correction in Higher-Dimensional Systems
The study published in Nature implemented qutrits and ququarts using a transmon qubit coupled to a superconducting microwave resonator. By introducing multiple photon modes into the cavity, researchers created a quantum system with multiple distinguishable levels of superposition.
To stabilize these states, the team used weak measurements via the transmon to detect drift in the quantum state without collapsing it, followed by feedback control based on reinforcement learning algorithms that dynamically optimized error mitigation parameters.
Key findings:
- A corrected qutrit achieved coherence times comparable to an uncorrected qubit.
- A corrected ququart outperformed an uncorrected qutrit.
- Error correction consistently improved the lifetime of all qudit types by a factor of ~1.8×.
This confirms that error correction is not exclusive to binary systems and can be extended to qudits with tailored strategies.
Why Qutrits and Ququarts Matter
The promise of qutrits and ququarts lies in their information density and potential resource savings:
- Fewer physical qudits needed to represent equivalent logical information.
- Reduced gate count in certain quantum algorithms re-engineered for higher bases.
- Enhanced fault-tolerant encodings, such as ternary or quaternary stabilizer codes.
- New cryptographic primitives enabled by multi-level quantum states, improving protocol robustness and key distribution efficiency.
In a world constrained by limited qubit yields, fabrication defects, and error rates, qudits offer a way to push the limits of current quantum hardware architectures.
Applications and Future Directions
Though still in the experimental stage, qutrits and ququarts are already being explored in:
- High-dimensional quantum key distribution (QKD)
- Simulation of naturally multi-level quantum systems (e.g., molecular systems, nuclear spins)
- Topological quantum computing, where qudit logic may simplify braiding and error-correcting schemes
- Quantum memory and repeaters, where fewer units can store more entangled information
Future research will focus on scalable control electronics, high-fidelity multilevel gates, and qudit-native algorithms to unlock their full potential.
Conclusion
While qubits remain the cornerstone of today’s quantum computing landscape, qutrits and ququarts represent a powerful evolution that could dramatically increase the efficiency, performance, and feasibility of practical quantum systems. The recent demonstration of qudit error correction is a significant step forward, showing that multi-level quantum logic is not only possible, but promising.
As the field progresses, quantum engineers may no longer ask, “How many qubits?”, but rather, “How many levels per unit?”—ushering in a new chapter of quantum computing beyond binary.
📘 Reference: Nature (2025), “Error-corrected memory in multilevel superconducting systems”, DOI: 10.1038/s41586-025-08899-y
source: Noticias inteligencia artificial